FrontEnd/알고리즘 및 코테
[알고리즘 JS] 버블정렬, 선택정렬, 삽입정렬 개념 및 비교!
- -
🐣 정렬
기본 내장 JavaScript 정렬
- 기본 정렬 순서는 문자열 유니코드(Unicode) 코드 포인트(code point)에 따름
- 배열의 모든 항목이 문자열로 변환되고, 해당 문자열의 유니코드 값이 선택되고, 그 다음에 항목이 정렬됨.
- 애초에 문자열로 정렬 시작하지 않는 한 원하는 결과 얻는게 힘듦
작동 방법
- 내장 정렬 메소드는 선택적 비교 함수(optional comparator function)를 인자로 전달 받음
- 이 함수를 사용해서 자바스크립트에 우리가 원하는 정렬 방식을 알릴 수 있음
- 기본적으로 이 함수는 A와 B라는 2개의 항목이 있는 구조로 작성
- 반환되는 값을 토대로 만들 정렬 순서를 자바스크립트에 알림
- 만약에 a와 b라는 2개의 항목이 있는 상태에서 음수를 반환하면, 자바스크립트는 두 항목을 비교할 때마다 이 함수를 호출
- 함수가 음수를 반환하면 자바스크립트는 a가 b 앞에 온다고 결정. 양수를 반환하면 그 반대.
- a가 b 뒤에옴.그리고 0을 반환하면, 자바스크립트는 a와 b를 동일하게 취급하고 한꺼번에 정렬하는데, 아무 상관 없음
예시1(숫자 기준 정렬)
function numberCompared(num1, num2){
return num1 - num2;
}
[6,4,15,10].sort(numberCompare);
// [4,6,10,15]- num1 - num2가 음수를 반환하면, num1이 num2 앞에 옴
- num1 - num2가 양수를 반환하면 num2가 num1 앞에 옴.
- 이렇게 하면 이제는 숫자가 오름차순으로 제대로 정렬
- 유니코드 문자를 사용하거나 그 밖의 여러 가지에 대해 걱정할 필요 없음
예시2(문자열 길이 기준 정렬)
function compareByLen(str1, str2){
return str1.length - str2.length;
}
["Steele", "Colt", "Data Structures", "Algorithms"].sort(compareByLen);- 문자열의 길이를 기준으로 정렬을 하는 것도 가능. 알파벳순으로 정렬하는 게 아님
- 제일 짧은 문자열부터 정렬. Colt에서 시작해서 제일 긴 문자열인 Data Structures에서 끝
- 다만 이 함수는 이 2개의 인자를 전달받아야 함 여기에 사용되는 인자. 반환하는 값은 음수나 양수 또는 0.
- str1.length - str2.length라고 작성하고, comparebyLen
🐣 버블 정렬
들어가기 전에
- 버블 정렬은 별로 효율적이지 않음
- 흔히 사용되지 않고, 유스케이스(use case) 하나 있음
- 빈번하게 구현하지 않지만 두각을 나타내는 분야가 있긴 함
- 다른 알고리즘이 버블 정렬보다 더 나은 이유를 이해하는데 도움

설명

- 버블 정렬의 개념은 배열을 가장 작은 숫자에서 가장 큰 숫자순으로, 그러니까 오름차순으로 정렬을 한다면 더 큰 숫자가 한 번에 하나씩 뒤로 이동.
- 참고 비주알고(VisuAlgo).
- 버블 정렬의 작동 방식은 루프를 돌면서 각 항목을 다음 항목(해당 항목의 오른쪽에 있는 항목)과 비교
- 숫자가 비교 대상보다 더 큰지 확인 후 교환(swap)
- 기본적으로 어떤 항목이 더 크면 교환을 하고, 다음 항목과 비교하고, 다음 항목보다 더 크면 또 교환을 하고, 다시 다음 항목과 비교
- 맨 앞에서부터 비교해서 들어감. 첫 번째로 배열을 끝까지 정렬하고, 다시 맨 앞에서부터 다시 과정 반복.
- 반복을 거듭함에 따라 우리가 정렬해야 하는 항목의 수가 감소(반복을 할 때마다 정렬할 항목이 줄어듦)
JS 교환 방법
// ES5
function swap(arr, idx1, idx2){
var temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
// ES2015
const swap = (arr, idx1, idx2) => {
[arr[idx1],arr[idx2]] = [arr[idx2], arr[idx1]];
}▷ 버블 정렬 구현
구현 1
- 루프를 시작. 즉, 함수를 정의. 명칭은 bubbleSort.
- 배열을 인자로 전달받는데, 전부 숫자라고 가정.
- i라는 변수를 가지고 배열의 맨 끝에서 루프를 시작해서 맨 앞에서 끝. 그 이유는 나중에 정확하게 설명.
- 우선은 정렬을 하고 있는 배열의 항목 수를 줄이는 것과 관련된다는 사실.
- 외부 루프 안에는 j라는 변수가 포함된 내부 루프. 내부 루프는 처음부터 i - 1까지 실행.
- i는 첫 번째 루프를 참조.
- 첫 번째 루프에 의존하는 중첩 루프라고 생각. i -1. 그러고 나면 그냥 arr[j]를 비교.
- 만약에 j가 0이면 이걸 arr[J+1]과 비교. 다음 항목임.
- j가 뭐든 간에, j를 그 다음 항목과 비교. j와 j+1을 비교.
- arr[j]가 arr[j+1]보다 더 크면 교환을 해야 한다는 의미
bubble_unoptimized.js
// UNOPTIMIZED VERSION OF BUBBLE SORT
function bubbleSort(arr){
for(var i = arr.length; i > 0; i--){
for(var j = 0; j < i - 1; j++){
console.log(arr, arr[j], arr[j+1]);
if(arr[j] > arr[j+1]){
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
// ES2015 Version
function bubbleSort(arr) {
const swap = (arr, idx1, idx2) => {
[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
};
for (let i = arr.length; i > 0; i--) {
for (let j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
return arr;
}
bubbleSort([8,1,2,3,4,5,6,7]);- i=0; i<arr.length 가 아니라
- i = arr.length; i > 0; i-- / var j = 0; j < i - 1; j++ 인 이유는 무의미한 비교를 하지 않기 위해서
- 맨 처음 배열 길이를 i로 시작. 만약 i가 4라면,
- 내부 : j가 i-1보다 작으면 j 증가 (즉 i가 4면 3번만 비교하면 됨)
- 외부 : 배열 길이 i에서 시작 0전까지 i 계속해서 --
- 내부 : j가 i-1보다 작으면이니까 i가 3됐으면, 2번만 비교
참고) 과정 설명
- 초기 배열: [8, 1, 3, 2]
- 첫 번째 패스 (i = 4):
- 비교 (8 > 1): [1, 8, 3, 2] (swap)
- 비교 (8 > 3): [1, 3, 8, 2] (swap)
- 비교 (8 > 2): [1, 3, 2, 8] (swap)
- 두 번째 패스 (i = 3):
- 비교 (1 > 3): [1, 3, 2, 8] (no swap)
- 비교 (3 > 2): [1, 2, 3, 8] (swap)
- noSwaps가 false이므로 계속 진행
- 세 번째 패스 (i = 2):
- 비교 (1 > 2): [1, 2, 3, 8] (no swap)
- noSwaps가 true이므로 정렬 완료
최종 배열
- 정렬된 배열: [1, 2, 3, 8]
▷ 버블 정렬 최적화
- 교환 항목이 없는데 계속해서 항목 정렬 실행 시도
- 루프가 마지막으로 실행 됐을 때 교환했는지 확인하고, 마지막에 교환을 하지 않았으면 정렬 완료된 것
optimized_bubble.js
// Optimized BubbleSort with noSwaps
function bubbleSort(arr){
var noSwaps;
for(var i = arr.length; i > 0; i--){
noSwaps = true;
for(var j = 0; j < i - 1; j++){
if(arr[j] > arr[j+1]){
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
noSwaps = false;
}
}
if(noSwaps) break;
}
return arr;
}
bubbleSort([8,1,2,3,4,5,6,7]);- noSwaps 만들어서 비교하는지 확인 후 처리
- 외부에 noSwaps 만들고
- 내부에 false 처리해서, 내부 if문 돌지 않았다면 반복문 바깥으로 나가짐. true인 상태이기 때문에 break.
▷ 버블 정렬 : 빅오 복잡도
- 일반적으로 n² / 중첩 루프, 대략적 비교
- 거의 정렬 or 이미 정렬 끝난 상태 noSwaps 변수 있으면 선형시간에 가까움
- 교환되지 않은 상태 확인하기 위해 다시 실행 후 루프 빠져나왔기 때문
- 가능한 최고의 경우 O(n)
- 위에서 살펴본 우리 예시는 2n, 간소화해서 O(n)
🐣 선택 정렬

설명
- 버블 정렬과 비슷하지만, 큰 값을 배열 끝에 위치시키는 대신
- 작은 값을 한 번에 하나씩 위치에 배열
- 처음부터 끝까지 움직이지만, 실제 정렬된 데이터는 처음부터 누적
- 최솟값을 찾아 마지막에 바꾸어 맨 앞에 둠.
- (예시) [5,3,4,1,2]가 있을 경우 5,3 비교 최솟값 찾고 / 3,4비교 최솟값 찾고.. 반복
- 첫 번째의 경우 [1,3,4,5,2]로 정렬 됨.
- 두 번째의 경우 [1,2,3,4,5]로 정렬 끝
- (예시) [44,5,38,19,47,15]의 경우 첫 번째 때, 5가 최솟값이라 44와 5 변경[5,44,38,19,47,15]
- [5,44,38,19,47,15] 두번째때 5는 이미 정렬됐기 때문에 44부터 시작. 새로운 최솟값은 15라서 44와 15 변경 [5,15,44,38,19,47]
- 위와 같은 방식으로 계속해서 정렬
- 진행하면서 가장 작은 요소, 즉 최솟값을 선택하고 맨 앞으로 배치
코드를 어떻게?
- 처음 해야할 것은 최솟 값을 저장할 변수 만들기
- 처음에는 최솟값 저장 변수 첫 번째 항목과 같게 설정(유일하게 확인된 값이기 때문)
- 다음에는 진행하면서 다음 항목과 비교하여 최솟값으로 갱신
- 실제로 변수에 저장하는 것은 값이 아닌 값을 찾은 인덱스
- (3번 인덱스가 최솟값일 경우) 첫 번째로 훑어본 다음 0번 인덱스를 3번 인덱스와 변경
- 계속해서 변경
▷ 선택 정렬 구현
selection_sort.js
// LEGACY VERSION (non ES2015 syntax)
function sselectionSort(arr){
for(var i = 0; i < arr.length; i++){
var lowest = i;
for(var j = i+1; j < arr.length; j++){
if(arr[j] < arr[lowest]){
lowest = j;
}
}
if(i !== lowest){
//SWAP!
var temp = arr[i];
arr[i] = arr[lowest];
arr[lowest] = temp;
}
}
return arr;
}
// ES2015 VERSION
function selectionSort(arr) {
const swap = (arr, idx1, idx2) =>
([arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]]);
for (let i = 0; i < arr.length; i++) {
let lowest = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[lowest] > arr[j]) {
lowest = j;
}
}
if (i !== lowest) swap(arr, i, lowest);
}
return arr;
}
selectionSort([0,2,34,22,10,19,17]);- for 반복문 안에 최솟값 담을 변수 만듦
- for 반복분 j는 i+1 (비교해야하기 때문)
- j와 최소값 비교하여 j가 더 작을 경우 최솟값 업데이트
- 참고로 최솟값은 value가 아니라 index
- 최솟값과 i 위치를 바꿔주기 위해 temp 이용
- if 변수에 i !== lowest 로 무의미한 반복 피하기(예를들면 첫번째 마주한 값이 lowest일 경우 반복 x도록)
- ES2015 ver에서는 swap 만들어서 temp 없이 바로 대입하도록
참고) 추가 과정 설명
- 초기 배열: [29, 10, 14, 37, 14]
- 첫 번째 패스 (i = 0):
- lowest = 0
- 비교 (29 > 10): lowest = 1
- 비교 (10 < 14): lowest = 1
- 비교 (10 < 37): lowest = 1
- 비교 (10 < 14): lowest = 1
- 10과 29 교체: [10, 29, 14, 37, 14]
- 두 번째 패스 (i = 1):
- lowest = 1
- 비교 (29 > 14): lowest = 2
- 비교 (14 < 37): lowest = 2
- 비교 (14 = 14): lowest = 2
- 14와 29 교체: [10, 14, 29, 37, 14]
- 세 번째 패스 (i = 2):
- lowest = 2
- 비교 (29 < 37): lowest = 2
- 비교 (29 > 14): lowest = 4
- 14와 29 교체: [10, 14, 14, 37, 29]
- 네 번째 패스 (i = 3):
- lowest = 3
- 비교 (37 > 29): lowest = 4
- 29와 37 교체: [10, 14, 14, 29, 37]
최종 배열
- 정렬된 배열: [10, 14, 14, 29, 37]
▷ 선택 정렬 : 빅오 복잡도
- 효율적이지는 않음 O(n^2)
- 선택 정렬이 버블 정렬보다 나은 시나리오는 단 하나, 스왑수를 최소화 하는 경우
- 버블 정렬의 경우 가장 큰값을 끝에 도달할 때까지 계속 바꾸면서 반복하여 비교 많이 하지만, 각 루프 끝날 때 한 번만 바꿈
- 어떤 이유로 메모리 고려, 실제 스왑 수행 고려할 경우 선택 정렬이 나을 수도 있음.
🐣 삽입 정렬

작동 방식
- 삽입 정렬은 배열의 과반을 점차적으로 만들어 정렬을 구축
- 과반은 항상 정렬
- 하나씩 이동하거나, 한 번에 가장 큰 요소를 찾거나 한번에 가장 작은 요소를 찾는 대신
- 각 요소를 취하여 정렬되어 있는 절반 속 해당되는 위치에 배치
- [3,44,38,5,47,15] 이렇게 있을 때 44의 경우 3보다 크기 때문에 원래 자리에 위치
- 38의 경우 44와 비교 했을때 44보다 작고, 3과 비교했을때 3보다 크기 때문에, 3과 44 사이에서 44보다 작기 때문에 [3,38,44,5,47,15]로 위치 변경
- 다음 5의 경우 [3,38,44,5] 이렇게만 봤을때 3과 38 사이에 들어가야 하기때문에 [3,5,38,44,47,15]로 변경
- 47의 경우 [3,5,38,44,47] 중에서 제 위치이기 때문에 가만히
- 마지막 15의 경우 [3,5,15,38,44,47]로 위치
- 첫 번째 요소는 정렬되어 있다고 가정하고, 두 번째 요소부터 올바른 위치에 삽입.
▷ 삽입 정렬 구현
insertion_sort.js
function insertionSort(arr){
var currentVal;
for(var i = 1; i < arr.length; i++){
currentVal = arr[i];
for(var j = i - 1; j >= 0 && arr[j] > currentVal; j--) {
arr[j+1] = arr[j]
}
arr[j+1] = currentVal;
}
return arr;
}
insertionSort([2,1,9,76,4])- i = 1로 해두는 이유는 추가로 반복하지 않기 위해서임. 0으로 해도 상관은 없지만 무의미한 반복.
- 처음부터 시작하는 것보다 배열의 끝이나 중간에서 진행하는게 더 쉽기 때문에 거꾸로 루프(실제로 거꾸로 수행해야 할 작업이 없기 때문에 쉬움)
- 만약 [1,2,9,76,0] 배열로 돌린다하면
- 1,2,9,76은 그대로고 0의 경우 재배열 필요
- i가 4 값일 경우 0값에 해당하는거고
- 이를 j = i-1값이랑 계속해서 비교 즉, 3,2,1,0번째랑 비교
- for반복 조건안에 arr[j]가 현재값보다 클때라고 해놨기 때문에 그럴 경우 arr[j+1]값에 j를 넣음
- [1,2,9,76,0] 일때 0과 76을 비교해서 76이 더 크기 때문에 arr[5]값에 arr[4]값을 넣음
- [1,2,9,76,76] 이렇게 됨. 0은 이미 currentVal에 저장했기 때문에 걱정 안해도 됨.
- 이렇게 계속해서 반복 후에 제 위치인 [0,1,2,9,76]로 가게 됨
참고) 추가 과정 설명
- 초기 배열: [2, 1, 9, 76, 4]
- 첫 번째 패스 (i = 1):
- currentVal = 1
- 비교 (2 > 1): [2, 2, 9, 76, 4] (2를 오른쪽으로 이동)
- arr[0] 위치에 1 삽입: [1, 2, 9, 76, 4]
- 두 번째 패스 (i = 2):
- currentVal = 9
- 비교 (2 ≤ 9): [1, 2, 9, 76, 4] (변경 없음)
- 세 번째 패스 (i = 3):
- currentVal = 76
- 비교 (9 ≤ 76): [1, 2, 9, 76, 4] (변경 없음)
- 네 번째 패스 (i = 4):
- currentVal = 4
- 비교 (76 > 4): [1, 2, 9, 76, 76] (76를 오른쪽으로 이동)
- 비교 (9 > 4): [1, 2, 9, 9, 76] (9를 오른쪽으로 이동)
- arr[2] 위치에 4 삽입: [1, 2, 4, 9, 76]
최종 배열
- 정렬된 배열: [1, 2, 4, 9, 76]
▷ 삽입 정렬 : 빅오 복잡도
- 가장 안 좋은 경우 O(n^2) 배열의 길이가 늘어날 수록 비교 횟수를 기본적으로 n제곱
- 삽입 정렬이 유리한 경우는
- 예를들어 온라인 알고리즘이라는 데이터가 있어서 데이터가 들어오는 대로 작동하는 알고리즘.
- 새로운 데이터를 수신하기 때문에 전체 배열을 한 번에 정렬할 필요가 없음.
- 예를들어 온라인에서 실시간으로 번호 제출하는 코드 받아서 정렬하려고 할 때, 삽입 정렬은 한 부분을 정렬된 배열로 유지하고 한 번에 항목을 삽입하여 작동하기 때문에
- 어떤 숫자가 입력되더라도 필요한 위치에 놓을 수 있음
- 라이브, 스트리밍 방식으로 들어온 데이터 즉시 입력하는 상황에 편리
🐣 정렬 기본 : 버블, 선택, 삽입 비교
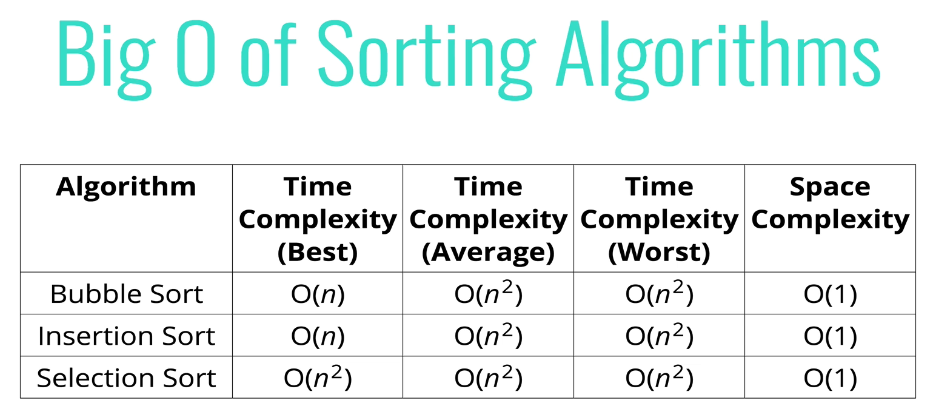
[시간 복잡도]
- worst 인 경우 모두 O(n^2)
- 정렬이 많이 되어 있는 경우 버블, 삽입은 O(n) : 정렬되어 있는 것들은 안 해도 되기 때문
- 선택의 경우 O(n^2) 왜냐하면 계속해서 순서대로 최솟값 찾기 때문
[공간 복잡도]
- O(1)
- 버블, 선택 및 삽입 정렬 알고리즘의 공간 복잡도는 O(1)
- 이러한 알고리즘이 요소를 제자리에 정렬하기 때문
- 즉, 입력 배열 자체 외에 일정한 양의 추가 메모리만 필요하기 때문
- 입력 크기에 따라 증가하는 추가 데이터 구조를 사용하지 않고 대신 요소 교환 및 인덱스 관리를 위한 몇 가지 추가 변수에 의존. 이렇게 하면 보조 공간이 일정하게 유지
버블, 삽입, 선택 한번에 정리해서 내용이 많지만..!_! 그래도 한번에 보는게 더 정리가 잘 되니까!
다음에는 합병, 퀵, 기수 정렬에 대해서 차례대로 각각 다뤄볼 것이당 !_! 내용이 많으니까!
[알고리즘 JS] 합병 정렬 (merge sort) 나누고 정복해!
🐣 합병 정렬[합병정렬자료](https://cs.slides.com/colt_steele/intermediate-sorting-algorithms)[sorting](https://visualgo.net/en/sorting?slide=1)[빅오](https://www.bigocheatsheet.com/) 설명기존의 버블,선택,삽입 정렬의 경우
haileyham.tistory.com
'FrontEnd > 알고리즘 및 코테' 카테고리의 다른 글
| [알고리즘 JS] 퀵 정렬(Quick sort)과 피벗(pivot) (0) | 2024.07.10 |
|---|---|
| [알고리즘 JS] 합병 정렬 (merge sort) 나누고 정복해! (0) | 2024.07.10 |
| [알고리즘 JS] 재귀(Recursion) (0) | 2024.06.30 |
| [알고리즘JS] 다중 포인터 패턴 (0) | 2024.06.26 |
| [알고리즘JS] 빈도 수 세기 패턴 (0) | 2024.06.26 |
Contents
소중한 공감 감사합니다
